ECUACIONES CON POTENCIAS FRACCIONARIAS

Exponentes fraccionarios: ½

En el ejemplo de arriba, el exponente es "2", ¿pero y si fuera "½"? ¿Cómo funcionaría?

Pregunta: ¿Qué es x^½ ?

Respuesta: x^½ = la raíz cuadrada de x   (o sea x^½ = √x)

¿Por qué?

Porque si calculas el cuadrado de x^½ tienes: (x^½)² = x¹ = x

Para entenderlo, sigue esta explicación de dos pasos:

1	Primero, hay una regla general: (xm)n = xm×n (Porque primero multiplicas x "m" veces, después tienes que hacer eso "n" veces, en total m×n veces) Ejemplo: (x2)3 = (xx)3 = (xx)(xx)(xx) = xxxxxx = x6 Así que (x2)3 = x2×3 = x6
2	Ahora, vemos qué pasa cuando hacemos el cuadrado de x½: (x½)2 = x½×2 = x1 = x Cuando hacemos el cuadrado de x½ sale x, así x½ tiene que ser la raíz cuadrada de x

Probamos con otra fracción

Vamos a probar otra vez, pero con un exponente de un cuarto (1/4):

¿Qué es x^¼?

(x^¼)⁴ = x^¼×4 = x¹ = x

Entonces, ¿qué valor se puede multiplicar 4 veces para tener x? Respuesta: La raíz cuarta de x.

Así que x^¼ = la raíz cuarta de x

Regla general

De hecho podemos hacer una regla general:

Un exponente fraccionario como 1/n significa hacer la raíz n-ésima:

Ejemplo: ¿Cuánto es 27^1/3 ?

Respuesta: 27^1/3 = 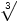27 = 3

¿Qué pasa con fracciones más complicadas?

Las fracciones más complicadas se pueden separar en dos partes:

• una parte con un número entero, y
• una parte con una fracción del tipo 1/n

Para entender eso, sólo recuerda que m/n = m × (1/n):

Así que tenemos esto:

Un exponente fraccionario como m/n significa haz la potencia m-ésima, después haz la raíz n-ésima

Ejemplo: ¿Cuánto es 4^3/2 ?

Respuesta: 4^3/2 = 4^3×(1/2) = √(4³) = √(4×4×4) = √(64) = 8