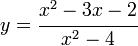Funciones Matemáticas: Conceptos Básicos

En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamadocodominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman elrecorrido, también llamado rango o ámbito).

Ver: Relaciones y funciones

En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”.

Las funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso.

A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?:

1 --------> 1

2 --------> 4

3 --------> 9

4 --------> 16

Los números de la derecha son los cuadrados de los de la izquierda.

La regla es entonces "elevar al cuadrado":

1 --------> 1

2 --------> 4

3 --------> 9

4 --------> 16

x --------> x².

Para referirse a esta regla podemos usar un nombre, que por lo general es la letra f (de función). Entonces, f es la regla "elevar al cuadrado el número".

Usualmente se emplean dos notaciones:

x --------> x² o f(x) = x² .

Así, f(3) significa aplicar la regla f a 3. Al hacerlo resulta 3² = 9.

Entonces f(3) = 9. De igual modo f(2) = 4, f(4) = 16, f(a) = a², etc.

Veamos algunos ejemplos que constituyen funciones matemáticas.

Ejemplo 1

Correspondencia entre las personas que trabajan en una oficina y su peso expresado en kilos

Conjunto X	Conjunto Y
Ángela	55
Pedro	88
Manuel	62
Adrián	88
Roberto	90

Cada persona (perteneciente al conjunto X o dominio) constituye lo que se llama la entrada o variable independiente. Cada peso (perteneciente al conjunto Y o codominio) constituye lo que se llama la salida o variable dependiente. Notemos que una misma persona no puede tener dos pesos distintos. Notemos también que es posible que dos personas diferentes tengan el mismo peso.

Ejemplo 2

Correspondencia entre el conjunto de los números reales (variable independiente) y el mismo conjunto (variable dependiente), definida por la regla "doble del número más 3".

x -------> 2x + 3 o bien f(x) = 2x + 3

Algunos pares de números que se corresponden por medio de esta regla son:

Conjunto X	Conjunto Y	Desarrollo
− 2	− 1	f(−2) = 2(−2) + 3 = −4 + 3 = − 1
− 1	1	f(−1) = 2(−1) + 3 = −2 + 3 = 1
0	3	f(0) = 2(0) + 3 = 0 + 3 = 3
1	5	f(1) = 2(1) + 3 = 2 + 3 = 5
2	7	f(2) = 2(2) + 3 = 4 + 3 = 7
3	9	f(3) = 2(3) + 3 = 6 + 3 = 9
4	11	f(4) = 2(4) + 3 = 8 + 3 = 11

Con estos ejemplos vamos entendiendo la noción de función: como vemos, todos y cada uno de los elementos del primer conjunto(X) están asociados a uno, y sólo a uno, del segundo conjunto (Y). Todos y cada uno significa que no puede quedar un elemento enX sin su correspondiente elemento en Y. A uno y sólo a uno significa que a un mismo elemento en X no le pueden corresponder dos elementos distintos en Y.

Ahora podemos enunciar una definición más formal:

Una función (f) es una regla que asigna a cada elemento x de un conjunto X (dominio) exactamente un elemento, llamado f(x), de un conjunto Y (codominio).

Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Y es una regla (o un método) que asigna un (y sólo uno) elemento en Y a cada elemento en X.

Usualmente X e Y son conjuntos de números.

Generalizando, si se tiene una función f, definida de un conjunto A en un conjunto B, se anota

f : A -----> B (o, usando X por A e Y por B f : X -----> Y) o f(x) = x

Recordemos de nuevo que el primer conjunto A se conoce como dominio (Dom) de la función y B es el codominio o conjunto de llegada.

f(x) denota la imagen de x bajo f, mientras que x es la preimagen de f(x).

En el ejemplo 2 anterior el número 3 es la imagen del número 0 bajo f; por su parte, 1 es la preimagen del número 5.

El rango (Rg) o recorrido (Rec) o ámbito (A) es el conjunto de todos los valores posibles de f(x) que se obtienen cuando x varía en todo el dominio de la función.

Ejemplo 3

Suponga que el conjunto A (de salida) es A = {1, 2, 3} y que el conjunto B (de llegada) es B = {0, 4, 6, 8, 10, 12} y que la relación de dependencia o correspondencia entre A y B es "asignar a cada elemento su cuádruplo".

Vamos a examinar si esta relación es una función de A en B y determinaremos dominio y recorrido.

Veamos:

A los elementos 1, 2 y 3 del conjunto A les corresponden, respectivamente, los elementos 4, 8 y 12 del conjunto B. Como a cada elemento de A le corresponde un único elemento de Y, la relación de dependencia es una función (función de A en B).

Dominio = {1, 2, 3} Recorrido = {4, 8, 12}

Notar que el recorrido es un subconjunto del codominio B = {0, 4, 6, 8, 10, 12}

Aquí debemos recordar que toda función es una relación, pero no todas las relaciones son funciones. Como ejemplos de relaciones que son funciones y algunas que no lo son, veamos las siguientes:

Si tenemos los conjuntos

A = {1; 2; 3; 4}, B = {1; 2; 3; 4; 5}

Podemos establecer las relaciones

f = { (1; 2); (2; 3); (3; 4); (4; 5) }

g = { (1; 2); (1; 3); (2; 4); (3; 5); (4; 5) }

h = { (1; 1); (2; 2); (3; 3) }:

Está claro que f, g y h son relaciones de A en B, pero sólo f es una función (todos los elementos del conjunto A tiene su correspondiente elemento en b); g no es función ya que (1; 2) y (1; 3) repiten un elemento del dominio (el 1). Tampoco h es una función ya que Dom(h) = {1; 2; 3} ≠ A (falta el 4).

Ejemplo 4

Sea X = {−4, −1, 0, 4, 9}, Y = {−4,−3, −2, −1, 0, 1, 2, 3, 4} y que la regla de correspondencia es " asignar a cada elemento de X el resultado de extraer su raíz cuadrada".

Vamos a determinar si esta regla constituye función de X en Y.

Veamos:

A simple vista se aprecia que los números 0, 4, 9 tienen imagen en Y (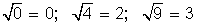

), pero a los números −4 y −1 no les corresponden elementos en Y. Como existen elementos de X que no se corresponden con elementos de Y, esta relación no es función de X en Y.

Dominio y rango de una función

Como ya vimos, el dominio de una función es el conjunto de valores para los cuales la función está definida; es decir, son todos los valores que puede tomar la variable independiente (la x).

Por ejemplo la función f(x) = 3x² – 5x está definida para todo número real (x puede ser cualquier número real). Así el dominio de esta función es el conjunto de todos los números reales.
En cambio, la función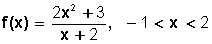

tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.

Si el dominio no se específica, debe entenderse que el dominio incluye a todos los números reales para los cuales la función tiene sentido.

En el caso de la función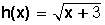

, el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.

Como resumen, para determinar el dominio de una función, debemos considerar lo siguiente:

Si la función tiene radicales de índice par, el dominio está conformado por todos los números reales para los cuales la cantidad subradical sea mayor o igual a cero.

Si la función es un polinomio; una función de la forma f(x) = a₀ + a₁x + a₂x² +...+ a_nxⁿ (donde a₀, a₁, a₂,..., a_n son constantes y nun entero no negativo), el dominio está conformado por el conjunto de todos los números reales.

Si la función es racional; esto es, si es el cociente de dos polinomios, el dominio está conformado por todos los números reales para los cuales el denominador sea diferente de cero.

El rango (recorrido o ámbito) es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.

Ejemplo

Identificar dominio y rango de la función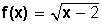

Veamos:

Como la función tiene radicales el dominio está conformado por todos los valores para los cuales x – 2 ≥ 0. Esto es, el dominio de la función incluye todos los reales que son mayores o iguales a 2.

El rango es igual al conjunto de los números reales positivos incluyendo el cero; puesto que al reemplazar los valores del dominio se obtienen únicamente valores positivos bajo la función f.

Dibuje un sistema de coordenadas en el papel cuadriculado para empezar a graficar funciones matemáticas. Nombre el eje vertical Y, y el eje horizontal X. Dependiendo de la ecuación, es posible que necesite utilizar una escala diferente. Las gráficas de la mayoría de las ecuaciones muestran la forma general de la gráfica y puntos de interés entre [-5, 5] y [-10, 10] para ambos ejes. Etiquete la intersección "0"

Dibuje un gráfico T para los valores en la ecuación. Un gráfico T fijará los valores de X y los valores correspondientes de Y. No pierda de vista los valores, cuando X = 0, y / o Y = 0. Por ejemplo, si la ecuación es: Y=2x + 1X | Y----------- -2 | -3-1 | -10 | 11 | 32 | 53 | 7

Escriba sus coordenadas basado en la tabla T. La tabla T: X | Y ----------- -2 | -3-1 | -10 | 11 | 32 | 53 | 7Se generan las siguientes coordenadas dando valores cercanos en la "X" cercanos a 0: (-2, -3), (-1, -1), (0,1), (1,3), (2,5) y (3,7).

Dibuje puntos en el diagrama de ejes que coincidan con sus pares de coordenadas. Empiece con los puntos que tienen un cero en cualquiera de los componentes (cero significa que están directamente encima del eje). En el ejemplo, vamos a comenzar con (0,1) y seguir dibujando los puntos en cualquier orden.

Revise los patrones en el gráfico. Si el patrón no está claro, repita los pasos 2, 3 y 4 hasta que pueda ver un patrón. El número de coordenadas puede variar dependiendo de la complejidad de su gráfico.

Utilice el lápiz para dibujar una curva que conecta todos los puntos. Asegúrese de que su curva sigue el esquema de eje. Trate de hacer la curva lo más suave posible.

Escriba la fórmula de la ecuación en la esquina superior derecha de su diagrama. En el ejemplo, la ecuación será y = 2x + 1, también se puede escribir F (x) = 2x + 1.

Sigue leyendo: http://educacion.uncomo.com/articulo/como-graficar-las-funciones-matematicas-basicas-1320.html#ixzz3qrKwEXW8

Dados dos conjuntos A y B, llamamos función a la correspondencia de A en B en la cual todos los elementos de A tienen a lo sumo una imagen en B, es decir una imagen o ninguna.

Función real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real.

f : D

x f(x) = y

El subconjunto en el que se define la función se llama dominio o campo existencia de la función. Se designa por D.

El número x perteneciente al dominio de la función recibe el nombre de variable independiente.

Al número, y, asociado por f al valor x, se le llama variable dependiente. La imagen de x se designa por f(x). Luego

y= f(x)

Se denomina recorrido de una función al conjunto de los valores reales que toma la variable y o f(x).

Conjunto inicial Conjunto final

Dominio Conjunto imagen o recorrido

El dominio es el conjunto de elementos que tienen imagen.

D = {x ∈ / ∃ f (x)}

El recorrido es el conjunto de elementos que son imágenes.

R = {f (x) / x ∈ D}

Dados los conjuntos X e Y, finitos o infinitos y una función f del conjuntoX en el conjunto Y que asigna a todo elemento x de X un solo elementoy de Y:

\begin{array}{rccl} f: & X & \longrightarrow{} & Y \\ & x & \mapsto & y = f(x) \end{array}

Dado un par de valores x de X e y de Y, tal que la función f los relaciona, x es el origen de la función e y la imagen. En el análisis de funciones tomaremos x como variable independiente e y como variable dependiente, y = f(x), la forma matemática de la expresión que relaciona x con y, da lugar a los distintos tipos de funciones, algunos de los cuales debido a su importancia, tienen nombres propios, y por las similitudes que presentan se pueden agrupar en tipos, a continuación podemos ver algunas de estas funciones o tipos de funciones, con las correspondientes referencias a los artículos principales donde son estudiadas en profundidad.

Función constante

Gráfica de una función lineal

En matemática se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable independiente. Se la representa de la forma:¹

f(x) = c \,

Funciones reales de una variable real

Como se puede ver es una recta horizontal en el plano cartesiano, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:

y = f(x) \,

tenemos:

y = c \,

donde c tiene un valor constante, en la gráfica tenemos representadas:

y = 8 \,

y = 4,2 \,

y = -3,6 \,

Como la variable dependiente y no depende de x tenemos que:

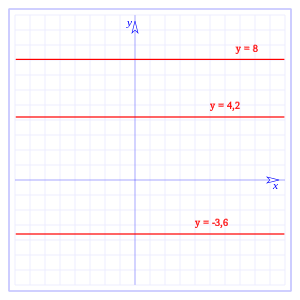
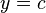
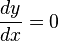
\frac{dy}{dx} = 0

la variación de y respecto a x es cero

La integral de la función constante:

y = c \,

es:

Y = \int_a^b c\,dx \; \rightarrow \quad Y = c \; \int_a^b dx \; \rightarrow \quad Y = c \; x \Big ]_a^b \; \rightarrow \quad Y = c \; (b-a)

Función lineal

¹ Texto en negrita

Para otros usos de este término, véase Función lineal (desambiguación).

No debe confundirse con Aplicación lineal.

Función lineal.

³ En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:

f (x) = mx + b

donde

m

b

son constantes reales y

x

es una variable real. La constante

m

es la pendiente de la recta, y

b

es el punto de corte de la recta con el eje

y

. Si se modifica

m

entonces se modifica la inclinación de la recta, y si se modifica

b

, entonces la línea se desplazará hacia arriba o hacia abajo.

Algunos autores llaman función lineal a aquella con

b = 0

de la forma:

f (x) = mx

mientras que llaman función afín a la que tiene la forma:

f (x) = mx + b

cuando

b

es distinto de cero, dado que la primera (

b = 0

) es un ejemplo también de transformación lineal, en el contexto de álgebra lineal.

Ejemplo

Dos rectas y sus ecuaciones en coordenadas cartesianas.

Una función lineal de una única variable dependiente

x

es de la forma:

y = mx + b

que se conoce como ecuación de la recta en el plano

x, y

En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

y = 0,5 x + 2

en esta recta el parámetro

m

es igual a

1 / 2

(correspondiente al valor de la pendiente de la recta), es decir, cuando aumentamos

x

en una unidad entonces

y

aumenta en

1 / 2

unidad, el valor de

b

2

, luego la recta corta el eje

y

en el punto

y = 2

En la ecuación:

y = - x + 5

la pendiente de la recta es el parámetro

m = -1

, es decir, cuando el valor de

x

aumenta en una unidad, el valor de

y

disminuye en una unidad; el corte con el eje

y

es en

y = 5

, dado que el valor de

b = 5

En una recta el valor de

m

se corresponde al ángulo

θ

de inclinación de la recta con el eje de las

x

a través de la expresión:

m = tanθ

$Función cuadrática$

Función cuadrática
Gráfica de Función cuadrática
Definición	$f(x) = ax^2 + bx + c \,$
Tipo	Curva parabólica
Dominio	$\mathbb{R}$
Imagen	$[\frac{4ac-b^2}{4a},+\infty) \text{o} (-\infty ,\frac{4ac-b^2}{4a} ]$
Cálculo infinitesimal
Derivada	$f'(x) = 2ax + b \,$
Límites	ninguno
[editar datos en Wikidata]

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida por:

y = ax^2 + bx + c \,

a \ne 0

También se da el caso que se le llame Trinomio cuadrático 2

Las gráficas de estas funciones corresponden a parábolas verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a >0, el vértice de la parábola se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a <0 el vértice se encuentra en la parte superior, siendo un máximo (es decir, la parábola se abre "hacia abajo").

El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico .

La función derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas .

Función racional

Este artículo trata sobre el concepto matemático. Para la «capacidad de razonar», véase Racionalidad.

Función racional de grado 2:

y = \cfrac{x^2 -3x -2}{x^2 -4}

Función racional de grado 3:

y = \cfrac{x^3 -2x}{2(x^2 -5)}

En matemáticas, una función racional de una variable es una función que puede ser expresada de la forma:

$f(x) = \frac{P(x)}{Q(x)}$

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen sudominio de definición en todos los valores de x que no anulen el denominador.¹ Esta definición puede extenderse a un número finito pero arbitrario de variables, usando polinomios de varias variables.

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

PORTAFOLIO PRECALCULO

sábado, 31 de octubre de 2015

GRAFICAR FUNCIONES

Funciones Matemáticas: Conceptos Básicos

Dominio y rango de una función

FUNCIONES

Función constante

Funciones reales de una variable real

Función lineal

Ejemplo

$Función cuadrática$

Función racional

Archivo del blog