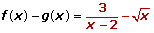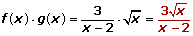Una ecuación es una igualdad que se cumple para algunos valores de las letras.
x + 1 = 2 x = 1
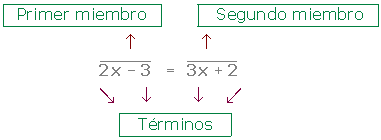
Elementos de una ecuación
Miembros
Los miembros de una ecuación son cada una de las expresiones que aparecen a ambos lados del signo igual.
Términos
Los términos de una ecuación son los sumandos que forman los miembros de una ecuación.
Incógnitas
La incógnita de una ecuación es el valor desconocido que se pretende determinar.
La incógnita de una ecuación se suele expresar con la letra x.
Soluciones
Las soluciones de una ecuación son los valores que deben tomar las letras para que la igualdadsea cierta.
2x − 3 = 3x + 2 x = −5
2 · (−5) − 3 = 3 · (−5) + 2
− 10 −3 = −15 + 2 −13 = −13
Grado
El grado de una ecuación es el mayor de los grados de los monomios que forman sus miembros.
Ecuaciones de primer grado
Las ecuaciones de primer grado son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.
Resolución de ecuaciones de primer grado
En general para resolver una ecuación de primer grado debemos seguir los siguientes pasos:
1º Quitar paréntesis.
2º Quitar denominadores.
3º Agrupar los términos en x en un miembro y los términos independientes en el otro.
4º Reducir los términos semejantes.
5º Despejar la incógnita.
Despejamos la incógnita:
Agrupamos los términos semejantes y los independientes, y sumamos:
Quitamos paréntesis:
Agrupamos términos y sumamos:
Despejamos la incógnita:
Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.
Quitamos paréntesis, agrupamos y sumamos los términos semejantes:
Despejamos la incógnita:
Quitamos paréntesis y simplificamos:
Quitamos denominadores, agrupamos y sumamos los términos semejantes:
Quitamos corchete:
Quitamos paréntesis:
Quitamos denominadores:
Quitamos paréntesis:
Agrupamos términos:
Sumamos:
Dividimos los dos miembros por: −9
Ecuaciones de segundo grado
Las ecuaciones de segundo grado son las expresiones de la forma:
ax2 + bx +c = 0 con a ≠ 0.
Para resolver ecuaciones de segundo grado utilizamos la siguiente fórmula:
Si es a<0, multiplicamos los dos miembros por (−1).
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado es incompleta si alguno de los coeficientes, b o c, o ambos, son iguales a cero.
ax2 = 0
La solución es x = 0.
ax2 + bx = 0
Extraemos factor común x:
ax2 + c = 0
Despejamos:


 .
. .
.

























 D g
D g
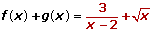
 − {2}
− {2} (2, ∞)
(2, ∞)